Phase MOSAIC can fit and manipulate data using Zernike polynomials. A description of these polynomials and their ordering can be found here.
![]()
![]()
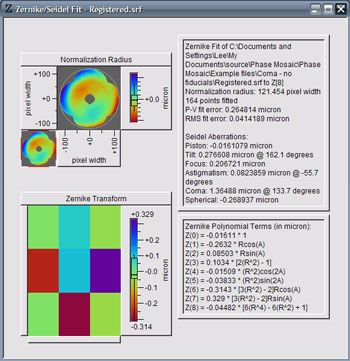
Zernike polynomial coefficients can be calculated for surfaces using the Analysis | Zernike/Seidel | Fit menu option. The resulting view window shows a list of the fitted coefficients int the lower right, the Zernike transform in the lower left, a representation of the normalization radius in the upper left, and statistics of the fit and interpreted Seidel coefficients are in the upper right.
| Normalization Radius | A 2D Surface View of the surface with a circle drawn at the current normalization radius used for the fit. The circle is centered on the coordinate system origin. |
| Coefficient list | List of fitted coefficients using the current Z axis units. |
| Zernike Transform | A 2-dimensional false-color representation of the coefficients. Coefficients are grouped in a square grid so that surface characteristics are apparent at a glance. Higher-order coefficients are in a line increasing from upper-left to lower-right. The upper-left corner contains the piston coefficient. Coefficients along the main diagonal represent pure radial structure. Lines parallel to the main diagonal represent various types of angular symmetric structure based on the distance from the main diagonal. The diagonal row of values next to the main diagonal have 1-theta dependence, the next 2-theta, etc. Upper diagonal values have sine dependence on this angular function, lower diagonal have cosine dependence. Details can be found here. |
| Fit Statistics | Shows the number of points actually fitted and the rms and peak to valley error between the these points and the surface. The actual number of points fitted will generally be different from the number of points specified in the Calculation Options dialog box to allow an evenly distributed sampling over the valid data points. |
| Seidel Coefficients | The inferred Seidel aberration coefficients and directions from the fitted Zernike coefficients. The angular convention defines 0 degrees to the right with angles increasing counter-clockwise (mathematical.) |
| Calculation Options | The maximum Zernike coefficient to fit can be specified, as well as the normalization radius to use. This is the radius of the unit circle used for fitting. By default, Phase MOSAIC will use the radius of the farthest valid data point from the coordinate system center. The desired number of points to sample can also be modified. More points can be specified for accuracy, however, the fit will take longer to calculate. |
If a mask is currently defined, aberrations can be fit using only valid data not covered by the mask. The mask does not need to be applied to the data. After a mask has been created in the 2D Surface View, choose Analysis | Zernike/Seidel | Masked Fit. A new fitting window will be created that uses the specified mask.
Masked fitting can be used to compare surfaces before and after manufacturing operations. Load both surfaces and mask regions that were modified on both. Use the same mask for each. Masked fit and remove any aberrations. Save both surfaces and subtract to calculate the effect of only the manufacturing operations.
New surfaces can be created using the Analysis | Zernike/Seidel | Generate menu item. Each type of generated surface can be optionally clipped to the currently defined normalization radius. This means valid data will only exist inside the unit circle used for the Zernike fit. Non-valid data from the current surface can also optionally be copied to the generated surface. These options are chosen using this dialog box before the surface is generated:
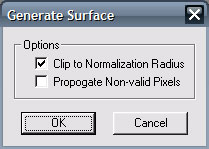
The surfaces that can be generated are:
| Fitted Surface | The currently fitted Zernike polynomial coefficients and normalization radius are used. |
| Zernike Surface | Arbitrary Zernike polynomial coefficents and normalization radius are specified using the Zernike polynomial editor. |