Surfaces can be represented by a linear combination of Zernike polynomials.

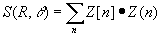
Z[n] are known as Zernike polynomial coefficients and have units of surface height. Positions are normalized to a unit circle radius so that the polynomials Z(n) are unitless (R = r / Normalization radius.)  Here is a partial listing of the Zernike polynomials used in Phase MOSAIC:

Z(0) = 1

Z(1) = R cos(q )

Z(2) = R sin(q )

Z(3) = 2 R² - 1

Z(4) = R² cos(2q )

Z(5) = R² sin(2q )

Z(6) = (3R² - 2) R cos(q )

Z(7) = (3R² - 2) R sin(q )

Z(8) = 6 R⁴ - 6 R² + 1

Z(9) = R³ cos(3q )

Z(10) = R³ sin(3q )

Z(11) = (4R² - 3) R² cos(2q )

Z(12) = (4R² - 3) R² sin(2q )

Z(13)= (10R⁴ - 12R² + 3) R cos(q )

Z(14) = (10R⁴ - 12R² + 3) R sin(q )

Z(15) = 20R⁶ - 30R⁴ + 12R² - 1

Note: In some Zernike numbering orders, the Zernike polynomial series is truncated at Z(35) and the next purely radial polynomial used in place of Z(36). This is not done in Phase MOSAIC. The following pure radial Zernike is Z(48).

The Seidel polynomials can be represented by linear combinations of Zernike polynomials. This means the magnitude of the Seidel polynomial coefficient can be calculated from Zernike polynomial coefficients. Phase MOSAIC adopts the common convention of using only the first eight Zernike coefficients to calculate Seidel coefficients:

Seidel Aberration	Magnitude	Angle
Piston
Tilt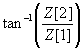
Focus
Astigmatism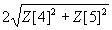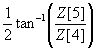
Coma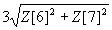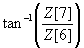
Spherical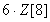

Other Resources